Nesta semana, darei continuidade ao tópico da última coluna (mercado de CDS), porém dessa vez falando como funciona a precificação desse mercado de derivativos de crédito. Vale (BVMF:VALE3) salientar que, apesar da relevância na proteção do risco de inadimplência e de expressivo volume global de operações, no Brasil há poucos registros de operações.
A fim de demonstrar como funciona a precificação, partiremos do exemplo apresentado na última coluna. Imagine que a empresa XYZ emitiu títulos a fim de financiar suas atividades de expansão. Vamos considerar que após minuciosa avaliação, você verificou uma forte possibilidade de calote no pagamento dos juros aos compradores dessa dívida emitida. Uma opção nesse caso é encontrar uma instituição financeira ou mesmo uma seguradora (vale salientar que a Resolução CMN 5.070 ampliou o leque de possíveis vendedores de CDS para instituições não financeiras, como seguradoras por exemplo) que esteja disposta a lhe vender um CDS da empresa XYZ. Para garantir essa proteção, você paga um prêmio, chamado de spread de risco de crédito (ou simplesmente spread do CDS), e isso permanece até o vencimento do contrato ou até que ocorra o default. O emissor é chamado de Entidade de Referência e o possível default de evento de crédito.
Suponhamos que o valor negociado com a instituição financeira foi de 200 milhões. Vamos assumir também que a taxa de recuperação do título (R) seja de 40%. Para viabilizarmos a precificação desse CDS é necessário estimarmos a probabilidade periódica (nesse caso anual) de default da Entidade de Referência. Existem algumas formas de estimar essa probabilidade, sendo uma delas observar o histórico de default de empresas com o mesmo rating. Para o nosso exemplo, vamos considerar que essa probabilidade seja de 2% a cada ano. Com as informações fornecidas, é possível calcular o spread pago anualmente sobre o valor do principal. Na figura abaixo, apresento a probabilidade de default como uma árvore binomial.
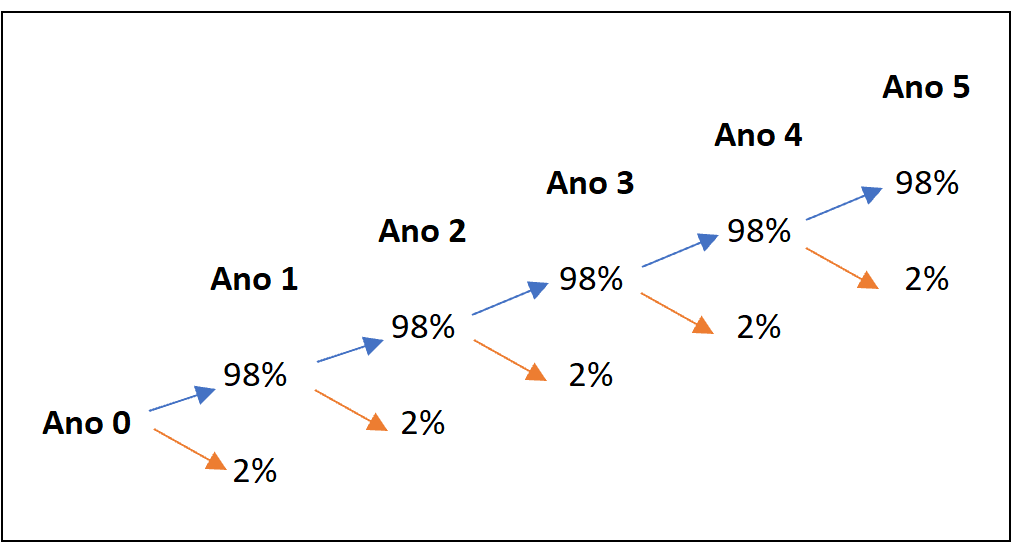
A partir dessa árvore, podemos calcular a probabilidade de default e não-default em qualquer ano. Por exemplo, vamos considerar o ano 3. A probabilidade de default exatamente no ano 3 seria: 98% (ano 1) x 98% (ano 2) x 2% (ano 3) = 1,92%. Já a probabilidade de não haver o default seria: 98% (ano 1) x 98% (ano 2) x 98% (ano 3) = 94,12%. Sendo assim, podemos estabelecer uma função geral. Considere p como a probabilidade de default, 1-p como não-default e n como o período de análise. A expressão geral para default seria calculada como (1-p)^(n-1) x p, enquanto o de não-default como é (1-p)^n. Utilizando essas expressões, vamos verificar as probabilidades do ano 5: i) default: (1-2%)^(5-1) x 2% = 1,84%; ii) não-default: (1-2%)^5 = 90,39%.
Com as probabilidades já estimadas, só falta estimar uma taxa de desconto que será utilizada para trazer os fluxos futuros esperados a valor presente. Considerarei o DI futuro para janeiro de 2029 de cerca de 10,65% (consulta realizada no site da B3 (BVMF:B3SA3)). A partir de então, é possível estimar o fator de desconto para cada período. Por exemplo, o fator de desconto do quarto ano será (1+10,65%)^(-4). Foi assumido que os pagamentos do CDS são realizados uma vez por ano e no final de cada ano. Vamos assumir também que caso tenha o default, que ocorra no final do ano.
As tabelas a seguir mostram a expectativa dos fluxos a pagar e a receber.
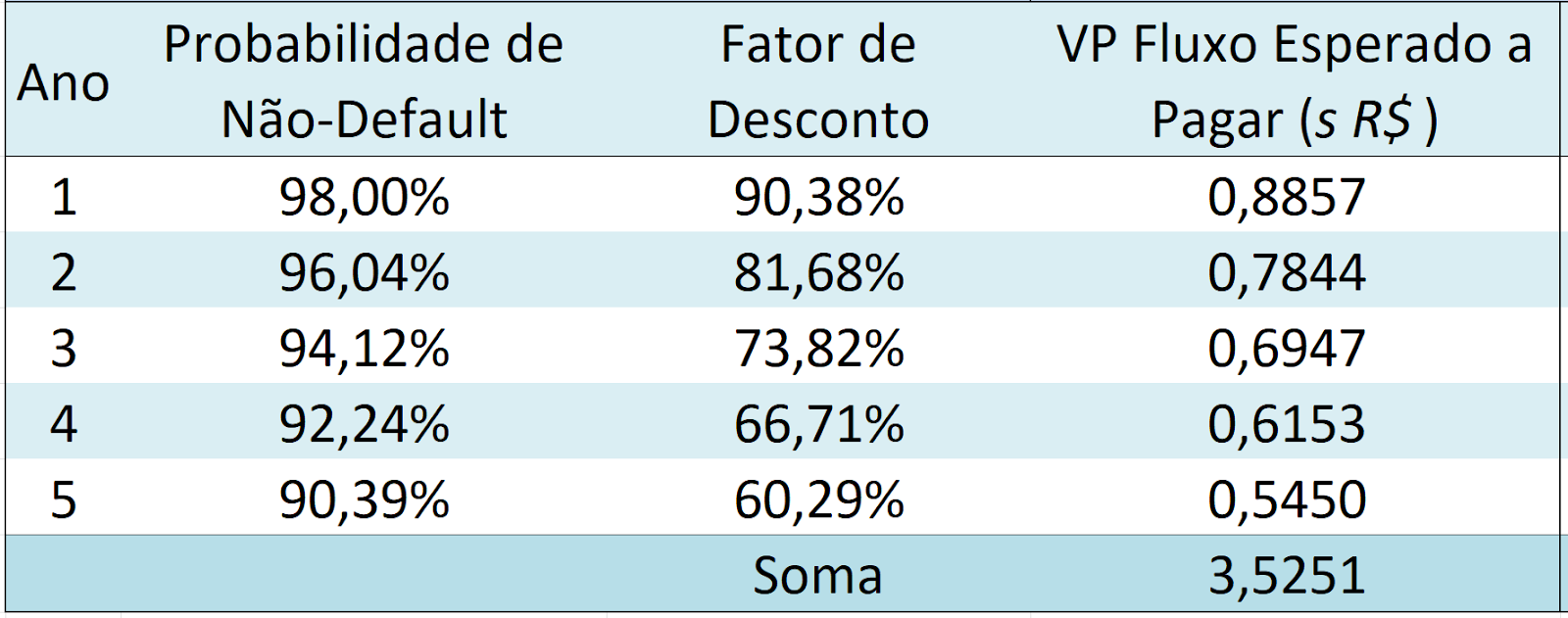
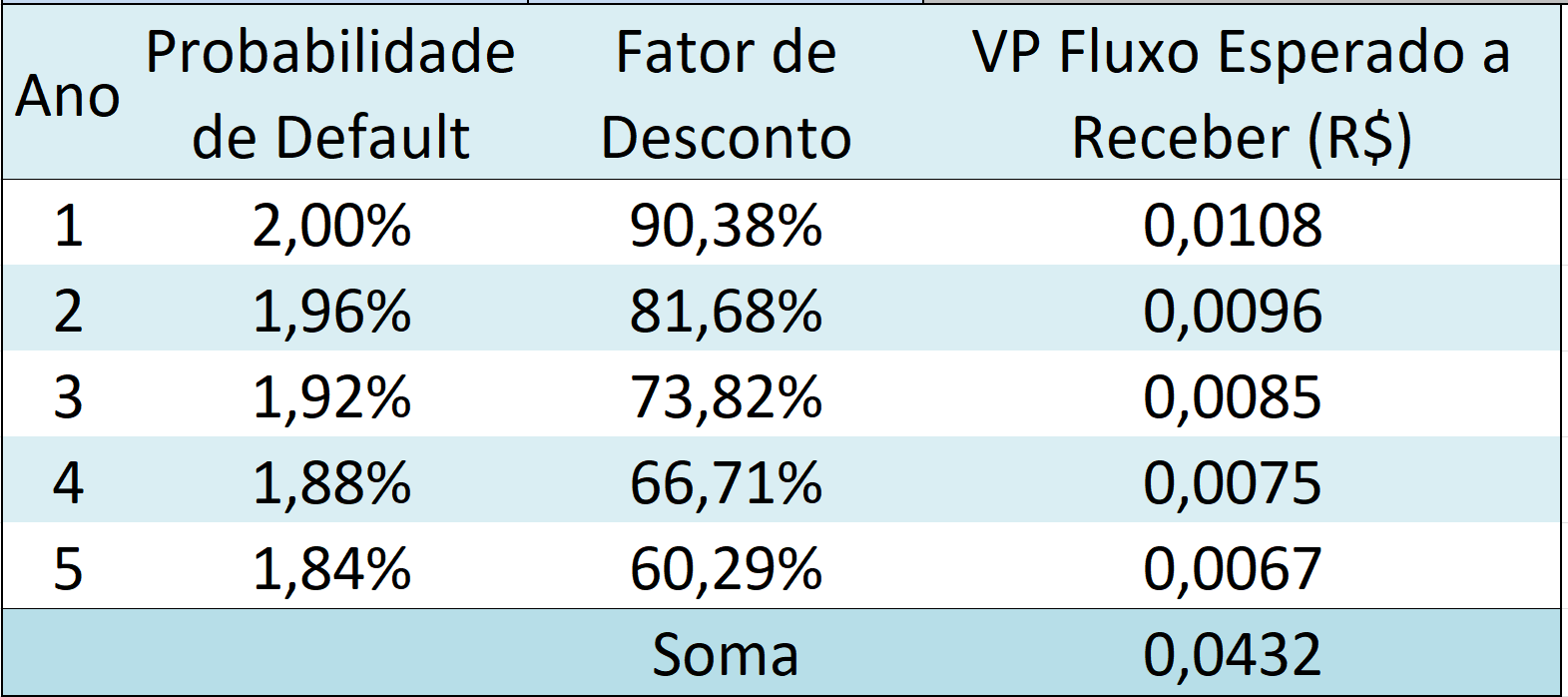
Para calcular o valor presente do fluxo a ser pago período a período, basta multiplicar a probabilidade de não-default pelo fator de desconto. Por exemplo, o fluxo do ano 3 será 94,12% x 73,82% = 0,6947s. Já para o fluxo esperado a receber, é necessário lembrar da taxa de recuperação de 40%. Sendo assim, para o mesmo ano 3, o fluxo esperado a receber é 1,92% x 73,82% x (1-40%) = 0,0085. Agora, basta igualar os fluxos esperados e encontramos o valor justo do spread pago periodicamente pela compra do CDS, ou seja:
![]()
Dessa forma, para as condições estimadas, concluímos que o spread a ser pago periodicamente é de 122 basis points por ano. Considerando o montante inicial de R$ 200 milhões, ao multiplicarmos esse valor pelo spread encontra-se um pagamento anual de R$ 2.448.979,59.
Caro leitor, na próxima coluna, abordarei como funciona a precificação desse mercado de derivativos de crédito, com exemplos numéricos de forma a consolidar o conhecimento no assunto. Caso tenha ficado alguma dúvida em relação ao assunto, fico à disposição por e-mail. Até a próxima!
