Arquimedes foi brilhante, não apenas por suas descobertas, mas igualmente por ter trabalhado em diversos campos da ciência, beirando um Leonardo da Vinci, entretanto há mais de 2.200 anos, ou seja, quase três séculos antes de Cristo. Ele é famoso pela história de sua descoberta da força de empuxo, afirmando que a força contra a qual um corpo imerso na água se submeteria seria igual ao peso da água deslocada. Reza a lenda que ele, ao fazer a descoberta, estaria se banhando e ficou tão empolgado que saiu correndo nu pelas ruas de Siracusa gritando “Eureca, Eureca, Eureca!” (“Achei, Achei, Achei!”).
A Arquimedes também é creditada a lei da alavanca e, segundo o filósofo e escritor grego Plutarco, deve-se a ele a famosa frase: “Deem-me um ponto de apoio que moverei a Terra”. Faz sentido, não? Na matemática, o gênio de Siracusa também desvendou teoremas importantes, seja no campo da teoria dos números, seja na geometria, na qual, em especial, ele era apaixonado pelas formas cônicas.
Dentre os muitos feitos de Arquimedes, ele descobriu que a área da superfície esférica seria precisamente igual à área lateral do cilindro que a circunscreve. Esse resultado foi extremamente impactante para a época e até hoje em dia causa alvoroço. Pensem que isso representa afirmar que a quantidade de tinta gasta para pintar uma esfera seria exatamente a mesma para pintar um papelão retangular que abrace a esfera por sua parte externa (na forma de um cilindro reto). Para facilitar o raciocínio, imagine uma bola do maior tamanho possível que caiba no pote cilíndrico abaixo:

A imensa maioria das pessoas que não recorressem às hoje conhecidas fórmulas matemáticas tenderia a dizer que a área do retângulo acima é maior que a área da “bola” (esfera), pois observe como ficaria a bola dentro do cilindro:
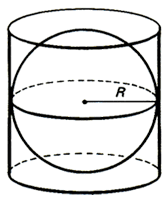
O raciocínio intuitivo que muitos teriam é: no meio do cilindro, numa faixa muito pequeninha, as áreas na esfera e no cilindro seriam praticamente iguais porque ambos encerram um círculo de mesmo raio. Mas fora da altura média, o círculo do cilindro é bem maior que o círculo equivalente da esfera. No limite, ou seja, nos dois polos (no extremo sul e no extremo norte), a esfera se reduz a um ponto de área zero enquanto o cilindro mantém sua circunferência idêntica. Portanto, afirmar que as áreas da esfera e do retângulo que dá origem ao cilindro acima são exatamente iguais causou quase o mesmo alvoroço que quando Nicolau Copérnico afirmou que a Terra não estava no centro do universo. Mas, lembre-se: Arquimedes estava há quase 300 anos antes de Cristo e muito antes da maioria das descobertas matemáticas. Na verdade, o ponto que resolve esse aparente paradoxo é que a “parede” a ser pintada da esfera é inclinada e, portanto, maior que a parede a ser pintada do cilindro, da mesma forma que a hipotenusa de um triângulo retângulo é maior que qualquer dos seus catetos. Isso compensa de forma exata o fato dessa “parede inclinada” ir ficando cada vez com raio menor na medida em que se aproxima dos polos da esfera.
E o que isso tem a nos ensinar com relação ao nosso processo de investir? Eu costumo dizer que o excesso de confiança é um dos piores inimigos do investidor porque ao se crer além da conta que sua estratégia de investimentos dará certo, tendemos a esquecer dos riscos. E ao esquecer dos riscos, tendemos a fazer apostas altas, pois só enxergamos o cenário no qual ganharemos muito dinheiro com quase nenhum esforço e resolveremos todos os nossos problemas financeiros. Isso é sedutor e pode nos cegar, podendo levar a perdas dramáticas. Acredite, já vi isso acontecer ao meu redor e não foi nem com uma nem com duas pessoas apenas!
Dessa forma, Arquimedes (e, por que não, Nicolau Copérnico) nos ensina(m) que devemos sempre lutar contra as obviedades, buscando o contraditório e entendendo as chances de nossas premissas (e crenças) estarem equivocadas ou, ao menos, imprecisas. Seja o seu próprio advogado do diabo! Afaste o excesso de confiança das suas decisões de investimentos, agindo sempre com cautela e entendendo que o mercado de investimentos é muito duro e não há oportunidades fantásticas sem um alto risco a correr. Não tenha o objetivo de “ganhar na Mega-Sena”, pois isso, fatalmente, te levará a perdas doloridas. Aliás, nesse momento sempre me vem à cabeça um ensinamento que costumam atribuir a Warren Buffet (e que eu desenvolvi um pouco, de forma livre):
“O problema é que as pessoas têm muita pressa para enriquecer, o que torna o jogo muito duro e desfavorável. É muito mais fácil enriquecer aos pouquinhos.”
Um forte e respeitoso abraço a todos. Fica o convite para seguir todo o conteúdo que produzo através do meu Instagram (@carlosheitorcampani).
* Carlos Heitor Campani é PhD em Finanças, Professor Pesquisador do Coppead/UFRJ – Cátedra Brasilprev e especialista em investimentos, previdência e finanças pessoais, corporativas e públicas. Ele pode ser encontrado em www.carlosheitorcampani.com e nas redes sociais: @carlosheitorcampani. Esta coluna sai a cada duas semanas, sempre na sexta-feira.
